Space Transform

Introduction :

     The space transformation calculation mainly depend on the conception and theory of linear algebra and analytic geometry in space , like vector, matrix, cross product and dot product, etc. The space transformation is a basic operation which can approximately be divided into two major groups, general and special. The general space transformation discuss translation, rotation and scaling. Thereinto, the rotation include the around fixed axis, the about an arbitrary axis, the Euler transform, the local coordination system alignment issue etc. The special space transformation refers to world transform, view space transform, clip space transform, tangent space transform, the transform from screen space to world space and so on. Those details is discussed below.

1.   Mathematical Tool

     Three orthogonal unit vectors each other that pass through same point erect a rectangular coordinate system in 3D space. A component of a arbitrary vector is the length which projects on a certain axis of the coordinate system. Depending on it, the transformation matrix of coordinates can be constructed which change a vector from one coordinate system into another.
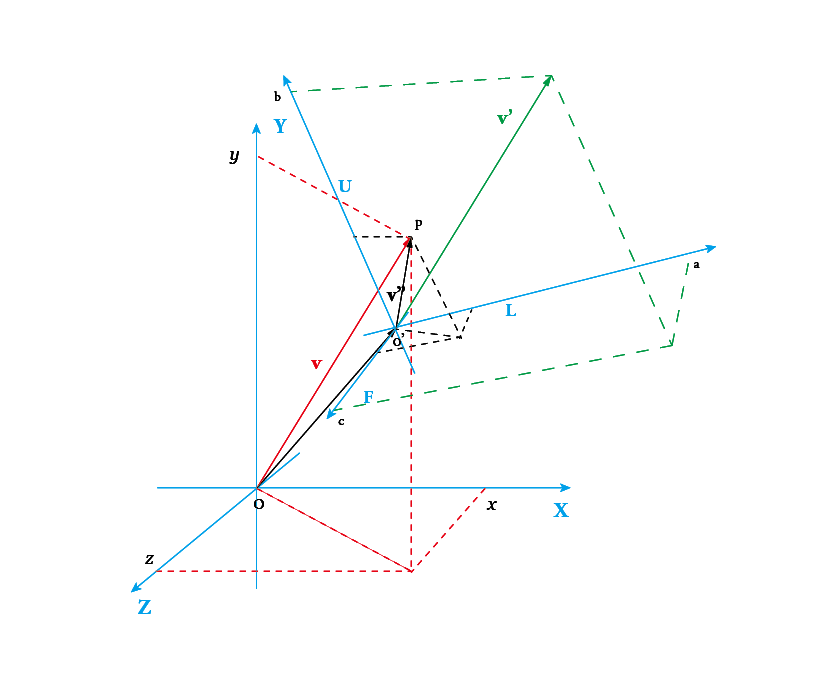
     Assume three unit vectors \(\mathbf{l, u, f}\) are orthogonal each other in the world space which create a LUF local space, \(\mathbf{v}\) is arbitrary vector in the world space, as follow:

Then, the vector transform formula can be built like this:

Where \(\mathbf{v'}\) is the LUF local space vector which is transformed from the vector \(\mathbf{v}\) in the world space (refer to Figure 1). In Figure 1, the vector \(\mathbf{v}\) own two coordinate sets, in the world space and LUF local space (the vector \(\mathbf{v'}\)).

     Assume \(\mathbf{p}\) is a point in the world space (refer to Figure 1), then the transform formula should be:

Where, \(\mathbf{M_{v4}}\) is the extended matrix of \(\mathbf{M_v}\), \(\mathbf{p'}\) is that point \(\mathbf{p}\) present in LUF coordinate system, \(\mathbf{M_p}\) is the transform matrix from world space into local space (LUF). If setup the 4th component of \(\mathbf{p}\) to zero, then \(\mathbf{M_p}\) can be used to transform direction vector in homogeneous space as well.

     Another interesting issue is how a local space point is transformed into world space if learning LUF base vector coordinate in the world space. It means that compute the inverse matrix of \(\mathbf{M_p}\) from known \(\mathbf{l, u, f, o'}\). Obviously, \(\mathbf{M_p}\) is not orthogonal matrix, solution of inverse matrix need use the corresponding adjoint matrix, that is very complex. In fact, if the projection of three base vectors, \(\mathbf{x, y,z}\) from world space into LUF space can be computed, the inverse matrix will be obtained by same solving of \(\mathbf{M_p}\). Observing, the projection of two vector each other have same length and the plus-minus sign, the coordinate of in world space just is opposite to \(\mathbf{o}\) in LUF space. Base on this two cases, \(\mathbf{M_p^{-1}}\)can be obtained more easily.

Where, \(\mathbf{o^{"}}\) is the LUF coordinate of original point \(\mathbf{o}\) , the deduction of \(\mathbf{M'_p}\) is same \(\mathbf{M_p}\).

2.   General Space Transformation

2.1Translation
     Translation is about space point primarily. In 4-Dimension homogeneous space, a point vector plus a off vector will generate a new location vector. Base on this, a translation computation is like:

3.   Special Space Transformation